1、泊松分布

由法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)在1838年时发表；

若X服从参数为的泊松分布，记为X~P()，

泊松分布的概率分布函数：

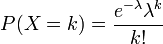
参数λ是单位时间(或单位面积)内随机事件的平均发生率。

统计学上，满足三个条件，即可用泊松分布

（1）小概率事件，两次以上事件发生概率趋于0；（2）事件发生的概率独立且互不影响；（3）发生概率时稳定的；

Poisson分布主要用于描述在单位时间(空间)中稀有事件的发生数，例如：

　　1.放射性物质在单位时间内的放射次数；

　　2.在单位容积充分摇匀的水中的细菌数；

　　3.野外单位空间中的某种昆虫数等。

二、二项分布

记作ξ~B(n,p) 期望：Eξ=np 方差:Dξ=npq

三、二项分布和泊松分布的关系（泊松分布的来源（泊松小数定律）

在二项分布的n次伯努利试验中，如果试验次数n很大，二项分布的概率p很小，且乘积λ= n p比较适中，则事件出现的次数的概率可以用泊松分布来逼近。事实上，二项分布可以看作泊松分布在离散时间上的对应物。

回顾e的定义：

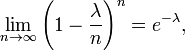
二项分布的定义：

如果令p=λ/n, p趋于无穷时的极限:

四、泊松分布与指数分布

泊松过程是一种重要的随机过程，适合于描述单位时间内随机事件发生的次数。泊松过程中，第k次随机事件与第k+1次随机事件出现的时间间隔服从指数分布。这是因为，第k次随机事件之后长度为t的时间段内，第k+1次随机事件出现的概率等于1减去这个时间段内没有随机事件出现的概率。而根据泊松过程的定义，长度为t的时间段内没有随机事件出现的概率等于

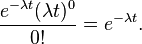
所以第k次随机事件之后长度为t的时间段内，第k+1次随机事件出现的概率等于，这是指数分布。这还表明了泊松过程的无记忆性。

五、最大似然估计

6、 指数分布比幂分布趋近0的速度慢很多,所以有一条很长的尾巴。指数分布很多时候被认为是长尾分布。互联网网页链接的出度入度符合指数分布。